2178번: 미로 탐색
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
www.acmicpc.net
이번 시간에는 BFS 탐색을 공부해보도록 한다.
미로 탐색 문제는 BFS 탐색의 기본을 닦을 수 있는 좋은 문제이다.

즉, 어떤 맵이 있어서 1이 통로이고, 0이 벽이다. 여기서 미로를 탐색할 수 있는 최단거리를 찾는 문제이다.
이게 또 미로라고 하니 옛날에 화면보호기라는게 있던 게 기억이 난다.
요즘은 화면보호기라는 말 자체가 안들리지만, 옛날에는 모니터의 수명이 짧았는데, 한 화면만 계속 틀고 있으면 해당 색의 화소가 타버려서 모니터가 금방 폐급이 되는 일이 있었다. (일종의 번인같은 현상)
그래서 화면보호기라고, 한 화면만 틀고 입력이 없으면, 자동으로 여러 화면을 틀어주어 화소들을 골고루 써주는 화면이 있었는데 그 중에서 가장 인상에 남는 것이 3D 미로였다.

직접 플레이할 수는 없고, 컴퓨터가 알아서 목적지까지 찾아가는 것을 보기만 했었는데, 미로에서 한쪽 벽에 손을 짚고 그 벽을 따라가면 언젠가는 목적지에 도착한다는 원리를 이용한 미로탐색이었다.
그래도 미로탐색하면서 여러 재밌는 요소(위아래가 뒤집어진다거나, 그림이 보인다던가) 가 있어서 보기만 해도 재밌었던 기억이 난다. (가끔은 일부러 화면보호기를 틀어놓고 보기만 했었다.)
옛날 얘기는 이정도로 하고.
무튼, 그냥 목적지를 탐색하는 거라면 한쪽 벽만 따라가도 될 것이나(이 경우는 DFS가 될 것이다.), 여기서는 최소 거리를 원하고 있다. 그렇기 때문에 BFS탐색으로 목적지까지 찾아가야한다.
그러면 일단 입력을 받아오고 기본 세팅을 해보자.
N, M = map(int,sys.stdin.readline().split())
maze = [list(map(int, list(str(sys.stdin.readline().rstrip())))) for _ in range(N)]
dx = [-1,0,1,0]
dy = [0,1,0,-1]
check = deque([[0,0]])
cnt = 1
dx, dy는 다들 아시다시피 2차원 행렬에서 사방(四方)으로 탐색하기 위해서 저리 설정을 해 놓았고,
check는 사방탐색을 실시할 기준점이다. (그래서 최초값으로 시작점인 (0,0)가 들어가있다.)
이 기준점에서 사방탐색을 실시하고, 만약 통로( 좌표의 값이 1)인 곳이 있으면 그 좌표를 check에 넣어줄 것이다.
그렇다면 왜 리스트가 아니라 deque인가? 그것은 조금 있다가 나올 것이다.
일단 코드를 진행해보자.
cnt += 1
for i in range(len(check)):
node = check.pop()
x = node[0]
y = node[1]
for d in range(4):
nx = x + dx[d]
ny = y + dy[d]check안에 있는 좌표를 꺼내줘서, x, y로 지정한다.
그 다음, for문과 dx, dy를 이용해서 사방탐색을 해준다.
(nx, ny) 의 값이 1이면, 우리는 그곳으로 진행해야하기에 리는 check에 (nx, ny)를 넣어줘야한다.
만약, 미로 탐색이 어느정도 진행되고, 어떤 (nx, ny)값이 목적지라면 우리는 현재 몇칸왔는지를 표시해주고 종료해줘야한다.
이게 미로탐색 문제의 전부이다.
while check:
cnt += 1
for i in range(len(check)):
node = check.pop()
x = node[0]
y = node[1]
for d in range(4):
nx = x + dx[d]
ny = y + dy[d]
if 0 <= nx < N and 0 <= ny < M and maze[nx][ny] == 1:
check.appendleft([nx,ny])
if nx == N-1 and ny == M-1:
print(cnt)
exit()미로탐색 코드의 기본 꼴은 위와 같다.
이제 여기서 유의점을 체크해보자.
이 단계가 시간초과 등의 문제가 일어나는 원인이 된다.
다음가 같은 경우가 있다.
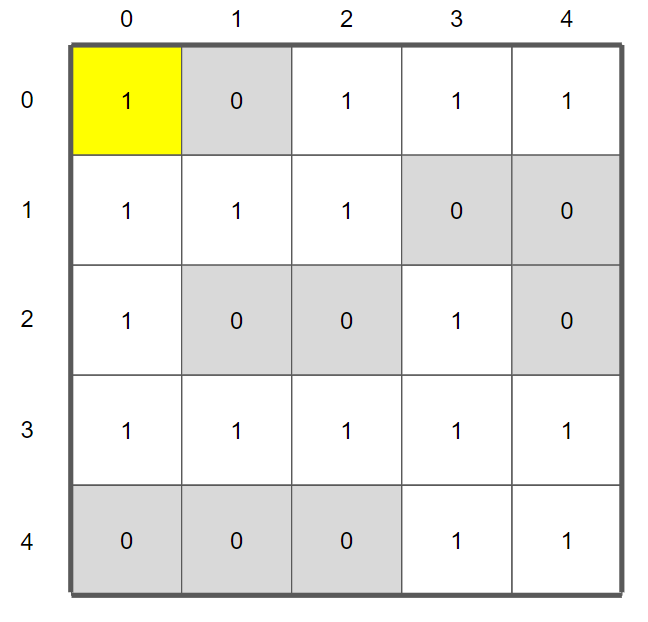
미로는 (0,0)에서부터 시작한다.
최초의 check는 (0,0) 이고, 현 단계에서 사방탐색을 해보자. 그렇다면 다음 좌표는 (1,0)이 될 것이다.
그러면 우리는 (0,0)을 빼주고 새로운 좌표 (1,0)을 넣어줘야한다.
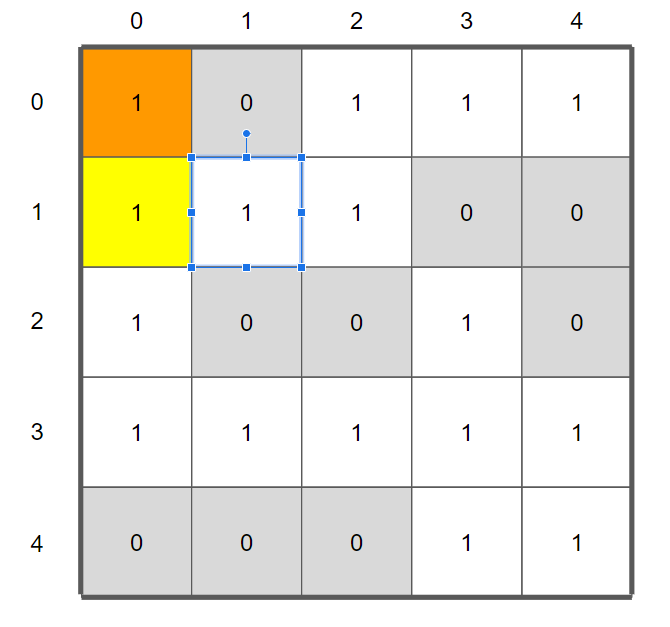
여기서 사방 탐색을 한다면 (2,1), (1,1)가 다음 check에 들어올 것이다.
(그리고 실은 주황색의 (0,0) 은 0으로 바꿔줘야한다. 그렇지 않으면, 여기서 (0,0)을 다시 check에 넣고 다시 (0,0)에서 다음 경로를 탐색할 것이기 때문에 엄청난 자원 손실이 일어날 것이다.)
사방탐색을 끝내고 나면 check = [[2,1], [1,1]]가 되어있다.
이제 다음 단계에서 왜 우리가 check를 리스트가 아닌 deque를 했는지 이유가 나온다.
다음 단계로 진행해보자.
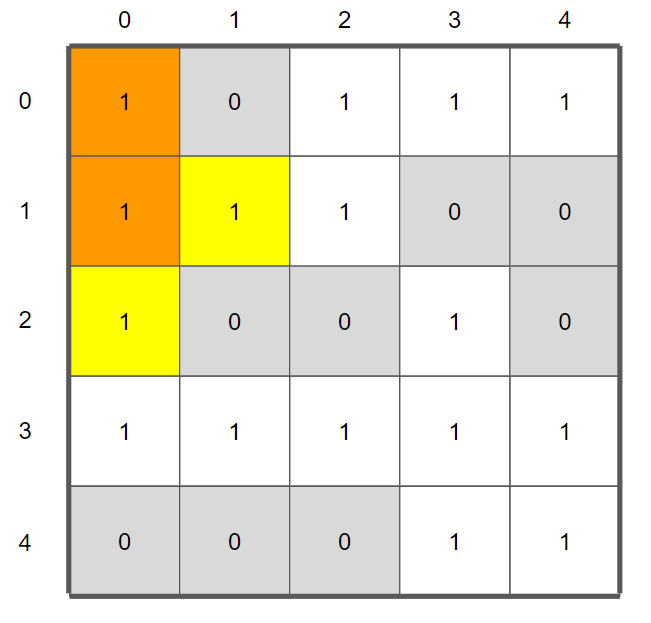
여기서 천천히 진행해보자.
현재 check = [[2,1], [1,2]]이다.
우리는 너비 우선 탐색을 하고 있기때문에 현 단계의 check 안에 있는 좌표들에 대해서 탐색을 '전부' 진행한 뒤에 다음 단계로 진행해야 한다.
하지만 check가 list라면 다음과 같은 문제가 발생한다.
일단 pop해보자. node = (1,1)가 된다. 그리고 (1,1)에서 갈 수 있는 단계는 (1,2)가 된다.
그러면 우리는 (1,2)를 list에 추가해줘야한다. 추가하면 check는 어떻게 되는가?
check = [[2,1]. [1,2]]가 된다.
문제점이 보이는가?
우리는 (1,2) 에서 탐색을 진행하고, 다음 좌표를 추가한 뒤에 (2,1)를 진행해야하나, 다음 좌표가 list의 끝부분에 있으므로 (2,1)이 아니라 (1,2)를 탐색하게 된다.
그 상태로 탐색을 진행한다면 다음 단계는 아래와 같다.

이러면 우리는 아랫쪽으로 진행하지 못하게 되고, 최단 거리 탐색도 할 수 없게 된다.
그래서 우리는 check를 deque형으로 써야하고, 사방탐색해서 다음 경로를 저장하는 경우에 appendleft로 앞쪽에 넣어줘야 한다. (물론, append로 오른쪽에 넣고 popleft로 왼쪽에서 꺼내도 된다.)
그리고 나도 미로탐색에서 시간초과로 고생했는데 원인은 다음과 같다.
다음 단계로 진행했을 때, 해당 좌표의 값을 0으로 바꿨었다. (아래 코드)
while check:
cnt += 1
for i in range(len(check)):
node = check.pop()
x = node[0]
y = node[1]
maze[x][y] = 0
for d in range(4):
nx = x + dx[d]
ny = y + dy[d]
if 0 <= nx < N and 0 <= ny < M and maze[nx][ny] == 1:
check.appendleft([nx,ny])
if nx == N-1 and ny == M-1:
print(cnt)
exit()단계를 옮기고 나서, maze[x][y] = 0을 한 것이 보이는가?
문제는 이거였다.
왜 문제가 되는지는 아래와 같다.
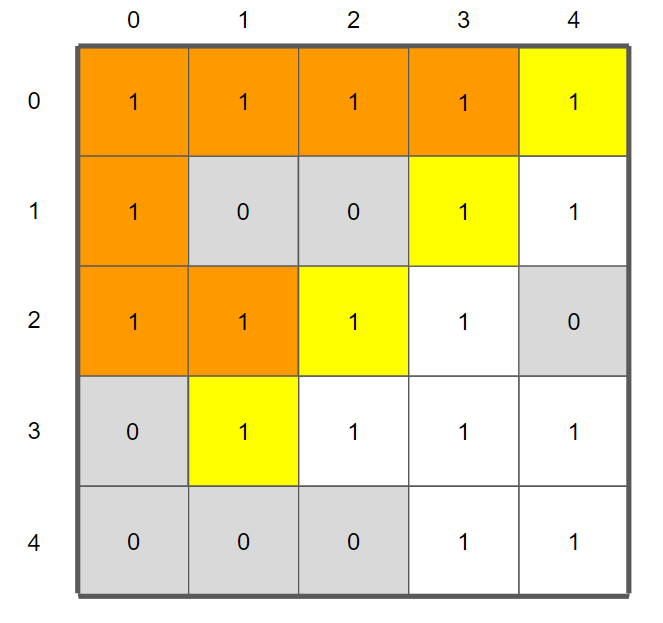
현 단계에서 check = [[0,4], [3,1], [2,2], [1,3]] 이다.
각 좌표에서 다음 단계를 탐색해보자.
(0,4) 의 경우 : (4,1) 를 추가
(3,1) 의 경우 : (4,1), (2,3) 를 추가
(2,2) 의 경우 : (2,3), (3,2) 를 추가
(3,1) 의 경우 : (3,2) 를 추가
문제점이 보이는가?
(4,1), (2,3) (3,2)가 중복되서 추가되는 것이 보인다.
check는 set형이 아니기 때문에 추가된 좌표에 대해서 모두 실행할 것이고 우리는 자원을 2배나 더 소모하고, 그 다음은 4배가 되어 엄청난 나비효과가 될 것이다. (이것이 시간초과가 나는 이유이다.)
코드를 바꿔줘보자.
if 0 <= nx < N and 0 <= ny < M and maze[nx][ny] == 1:
check.appendleft([nx,ny])
maze[nx][ny] = 0
위와 같이, 다음 통로를 탐색했을 때, 다음 좌표를 check에 추가해주고 동시에 추가한 좌표를 0으로 바꿔야 위와 같은 중복 탐색을 예방할 수 있다.
완성된 코드는 다음과 같다.
import sys
from collections import deque
N, M = map(int,sys.stdin.readline().split())
maze = [list(map(int, list(str(sys.stdin.readline().rstrip())))) for _ in range(N)]
dx = [-1,0,1,0]
dy = [0,1,0,-1]
check = deque([[0,0]])
maze[0][0] = 0
cnt = 1
while check:
cnt += 1
for i in range(len(check)):
node = check.pop()
x = node[0]
y = node[1]
for d in range(4):
nx = x + dx[d]
ny = y + dy[d]
if 0 <= nx < N and 0 <= ny < M and maze[nx][ny] == 1:
check.appendleft([nx,ny])
maze[nx][ny] = 0
if nx == N-1 and ny == M-1:
print(cnt)
exit()
'프로그래밍 공부 > 백뚠' 카테고리의 다른 글
| 토이스토리 (백준 2637 : 장난감 조립) (0) | 2020.12.29 |
|---|---|
| 따봉도치는 고마워! (백준 3055:탈출) (0) | 2020.12.29 |
| 몸에도 좋고 맛도 좋은 (백준 3190 : 뱀) (1) | 2020.12.22 |
| 땅! 땅! 땅! 빵! (백준 8983 : 사냥꾼) (0) | 2020.12.21 |
| 레이저 타워 디펜스 (백준 2493 : 탑) (0) | 2020.12.21 |


댓글